Lifting points, to provide adjustable lifting centres, to handle out of balance loads, to remove or control inward or crushing forces, to allow for special load attachments. Calculations to be made will include the capacity, both of the overall beam and of the loading of the individual lifting points. Attribution Non-Commercial (BY-NC) Available Formats. Download as XLS, PDF, TXT or read online from Scribd. Flag for inappropriate content. Save Save Lifting lug calculation.xls For Later. 80% (5) 80% found this document useful (5 votes) 11K views 3 pages.
Page 4 STANDARD LIFTING LUG DESIGN 20 TONS CAPACITY Generals: total weight (Empty Skid + lifted equipment) = number of lifting points = Safety Factor, FS = Min. sling angle, q = Max. load per lifting lug =
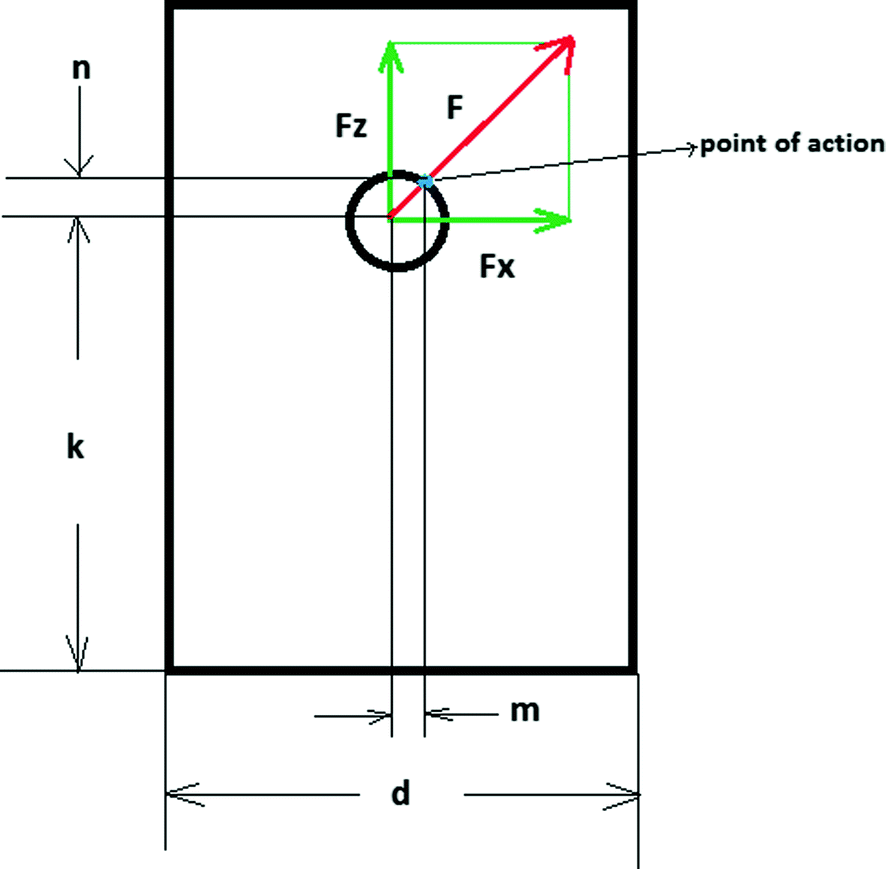
Lug Dimensions: Height of hole centreline, H = Width of Lug, W L = Radius of Lug, R = Diameter of Hole, DH = Thickness of Lug, tL = Allowable Stresses: Lug Material Allowable Tension Stress, 0.6 x Fy = Allowable Shear Stress, 0.4 x Fy =
20000 kgs = 1 2.0 60 degrees 40,000 kgs =
44,092 lbs
88,184 lbs
120 mm = 300 150 60 28
4.72 inch
mm = mm = mm = mm =
11.81 5.91 2.36 1.10
A 36 Fy = 1,519 Kg/cm2 = 1,012 Kg/cm2 =
inch inch inch inch
36,000 psi 21,600 psi 14,400 psi
DH/2R = 0.20 Stress-Concentration Factor (near hole), K = 2.5 (for flat plate with centrally located circular hole in tension based on DH/2R value)
Tension Stresses in the Lug: Weight in each Lug, W = Cable Tension at Lug, F = Inertia Moment of Lug, IL = Stress at Lug to Beam Joint = ST = F.cos (q). H.(W L/2)/IL +
40,000 kgs = 46,188 kgs = 6,300 cm4 = 1,136 Kg/cm2 =
F.sin(q)/(W L.tL) Stress at near the hole = ST = K .F. sin (q) / [(2.R -DH).tL]
88,160 lbs 101,798 lbs 151.36 in4 16,153 psi Safe
Ratio =
Safe
21,160 psi Ratio = 97.96%
Safe
3,909 psi Ratio = 27.15%
Safe
4,887 psi Ratio = 33.93%
1,488 Kg/cm2 =
74.78%
Shear Stresses in the Lug: Stress at Lug to Beam Joint = SS = F.cos(q) / (tL.W L)
275 Kg/cm2 =
Stress at near the hole = SS = F.cos(q) / [(2.R - DH).tL]
344 Kg/cm2 =
Page 5
Stresses in Weld: The calculation used is conservative as it only includes top fillet welds (actual stresses are lower) Leg size of fillet weld, LW = use 45 degree fillet weld Throat size of fillet feld, tW =
17.68 mm =
0.70 in
Length of weld, Ww1 = 2.W L + 2.tL
656.0 mm =
25.83 in
1,743.4 mm =
68.64 in
530,330 mm3 =
32.36 in3
Length of weld including welding in web of beam, W
25.0 mm =
0.98 in
W w2 = W w1 + W L + 2.Hbeam Section Modulus of weld lines, SW = SW= tw.W L2/3 Efficiency of weld, n = Allowable Load on weld Tension Stress at the weld = ST=[F.cos(q).H/SW+ F.sin(q)/ (W w2.tw)] / n Shear Stress at the Weld = ST=[ F.cos(q)/ (W w1.tw)]/ n
100% 675 Kg/cm2 =
9,600 psi
652 Kg/cm2 =
9,276 psi Safe
Ratio =
Safe
2,832 psi Ratio = 29.50%
30.86 Kg/cm2 =
96.62%
Lug Dimensions: Height of hole centreline, H = Width of Lug, W L = Radius of Lug, R = Diameter of Hole, DH = Thickness of Lug, tL = Allowable Stresses: Lug Material Allowable Tension Stress, 0.6 x Fy = Allowable Shear Stress, 0.4 x Fy =
20000 kgs = 1 2.0 60 degrees 40,000 kgs =
44,092 lbs
88,184 lbs
120 mm = 300 150 60 28
4.72 inch
mm = mm = mm = mm =
11.81 5.91 2.36 1.10
A 36 Fy = 1,519 Kg/cm2 = 1,012 Kg/cm2 =
inch inch inch inch
36,000 psi 21,600 psi 14,400 psi
DH/2R = 0.20 Stress-Concentration Factor (near hole), K = 2.5 (for flat plate with centrally located circular hole in tension based on DH/2R value)
Tension Stresses in the Lug: Weight in each Lug, W = Cable Tension at Lug, F = Inertia Moment of Lug, IL = Stress at Lug to Beam Joint = ST = F.cos (q). H.(W L/2)/IL +
40,000 kgs = 46,188 kgs = 6,300 cm4 = 1,136 Kg/cm2 =
F.sin(q)/(W L.tL) Stress at near the hole = ST = K .F. sin (q) / [(2.R -DH).tL]
88,160 lbs 101,798 lbs 151.36 in4 16,153 psi Safe
Ratio =
Safe
21,160 psi Ratio = 97.96%
Safe
3,909 psi Ratio = 27.15%
Safe
4,887 psi Ratio = 33.93%
1,488 Kg/cm2 =
74.78%
Shear Stresses in the Lug: Stress at Lug to Beam Joint = SS = F.cos(q) / (tL.W L)
275 Kg/cm2 =
Stress at near the hole = SS = F.cos(q) / [(2.R - DH).tL]
344 Kg/cm2 =
Page 5
Stresses in Weld: The calculation used is conservative as it only includes top fillet welds (actual stresses are lower) Leg size of fillet weld, LW = use 45 degree fillet weld Throat size of fillet feld, tW =
17.68 mm =
0.70 in
Length of weld, Ww1 = 2.W L + 2.tL
656.0 mm =
25.83 in
1,743.4 mm =
68.64 in
530,330 mm3 =
32.36 in3
Length of weld including welding in web of beam, W
25.0 mm =
0.98 in
W w2 = W w1 + W L + 2.Hbeam Section Modulus of weld lines, SW = SW= tw.W L2/3 Efficiency of weld, n = Allowable Load on weld Tension Stress at the weld = ST=[F.cos(q).H/SW+ F.sin(q)/ (W w2.tw)] / n Shear Stress at the Weld = ST=[ F.cos(q)/ (W w1.tw)]/ n
100% 675 Kg/cm2 =
9,600 psi
652 Kg/cm2 =
9,276 psi Safe
Ratio =
Safe
2,832 psi Ratio = 29.50%
30.86 Kg/cm2 =
96.62%
62
Description
Lifting Lug Design Calculation Pdf

Check lug shear stress.
Check Bending and tension stress.
Check bearing stress.

Lifting Lug Calculation Pdf
Check weld size.
Calculation Reference
Machine Design
Strength of Welds
Design of Lifting Equipment
Calculation Preview
21 Mar 2011
39.50 Kb
448
1.0
62
This download is for Registered Users Only.
Perhaps you need to login or register.
×
The equation seems appropriate. My concern is the coding in the excel spreadsheet in which leaving out the parenthesis makes a significant difference.
nice
I don't know if it is addressed in this thread, but G16 has an error in it regarding the calculation of the horizontal component of the load based on theta. I believe the equation should be G18*cos(G17*PI()/180)
I am sorry pgrahn I thought it was a question only relating to cell D59 regarding the combined stress but I now realise the question relates to cell D31 and I must say I am a little perplexed too. The first two terms seem fine but I am not at all sure what the third term in the equation is doing. To my mind there seems to be confusion between the resultant force Fr and vertical and horizontal components Fv and Fh. I hope that the author shaberli can shed some light on the calculation but I would be extremely cautious about its use in my own calculations. There are many other lug calculations on the site with good ratings and feedback perhaps you should take a look to them?
The equation seems appropriate. My concern is the coding in the excell spreadsheet in which leaving out the parenthesis makes a significant difference.
Without the parenthesis in the denominator the numerator is only divided by 'W' and not '(W*(t^2/6)).
The author may have multiplied t instead of squared t as well.
The formula for combined stress seems to be an approximation for either the maximum principle stress or twice the maximum shear stress. Both of which are used for failure criterion. I do not think it is a mistake. You could study further using Biaxial Stress Assessment.xls. A set of brackets is redundant in the formula but this matters little to the result. It will be interesting to see calculation author's comments.
I have a question/concern about calculating the Bending + Tension Stress (Longitudinal)equation.
In the denominator of the last equation it has '(W*(t2/6)'...
Is that t^2 or t*2?
Also in the excell equation is leaves out a set of parenthesis.
These two possible errors results in dramatic changes in the equation.
In the denominator of the last equation it has '(W*(t2/6)'...
Is that t^2 or t*2?
Also in the excell equation is leaves out a set of parenthesis.
These two possible errors results in dramatic changes in the equation.
Hi I am an ExcelCalcs website administrator. Could you explain the problem you are having and I can try to help you. What are you trying to do?
barangeravindra emailed saying:
We try to help as best we can but we simply do not have enough time to answer such detailed questions from free subscribers. However our calculations previews in this folder show the equations you are looking for. Please feel free to copy the formulas into your own spreadsheet.
barangeravindra emailed saying:
We try to help as best we can but we simply do not have enough time to answer such detailed questions from free subscribers. However our calculations previews in this folder show the equations you are looking for. Please feel free to copy the formulas into your own spreadsheet.
Comments are closed.